31:
Here’s that time of the year when you make those resolutions you’ll never gonna keep. I’ll make mine and I’ll try to stick to it, hopefully. Well, what is it? Very simple: I want to practice more and more regularly live coding in SuperCollider AND record audio sessions, and post them here in a section called “L!vE K@ding”. I’m not sure I will be posting codes about it, though, ’cause when I live code I get very messy. But I’ll be happy to discuss techniques, etc., what I do, and don’t. Let me add I’m not an expert at all, and there’s some great people out there doing excellent things. But you know what? If you never start, you’ll never learn. The session is not perfect? Who cares, that’s how “live” is. 😉
So, watch this space, if you are interested.
Meanwhile, Happy New Coding Year!
20:
In this post I want to talk about musical phrasings in algorithmic composition and algebra over finite fields. Yep, algebra, so brace yourself :-).
I am pretty sure you have been exposed to clock arithmetic: basically, you consider integer numbers modulo a natural number p. Now, in the case p is a prime, the commutative ring 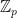 is actually a field with finite elements. There is a name for that, and it is finite field, or Galois* field.
is actually a field with finite elements. There is a name for that, and it is finite field, or Galois* field.
Now consider a pxp-matrix A with entries in 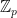 : A will give us a map
: A will give us a map  from
from 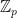 to itself via
to itself via

where  are the entries of A. Now, consider a function f from
are the entries of A. Now, consider a function f from 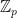 to a finite set S, and consider the subgroup P of the group of permutations of p objects given by elements
to a finite set S, and consider the subgroup P of the group of permutations of p objects given by elements 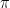 satifying
satifying

If the function f is not injective, this subgroup will be not empty. Notice that for any function f of the type above, the matrix A gives us another function  defined as**
defined as**
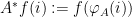
Now we can ask ourselves: given a function f, can we find a matrix A such that

for some natural number k? What this means is that we want to find a matrix such that applied k-times to the function f returns the function itself. This problem is equivalent to finding a matrix A such that

In the case in which the function f is injective, this coincides with the problem of finding idempotents matrices in a finite field: the fantastic thing is that they are known to exist***, and even better their number is known in many situations!
“Ok, now, what all of this has to do with musical phrasing?! No, seriously, I’m getting annoyed, what really? ”
I hear your concern, but as with almost everything in life, it’s just a matter of perspective. So, consider the set S as a set of pairs (pitch, duration) for a note. A function f above will tell us in which order we play a note and what is the duration of each note: in other words, it is a musical phrasing. By picking a matrix A, we can generate from f a new phrasing, given by the function  , and we can reiterate the process. If A is such that it satisfies the condition above, after a finite number of steps, the phrasing will repeat. Hence, the following Supercollider code
, and we can reiterate the process. If A is such that it satisfies the condition above, after a finite number of steps, the phrasing will repeat. Hence, the following Supercollider code
s.boot;
SynthDef(\mall,{arg out=0,note, amp = 1;
var sig=Array.fill(3,{|n| SinOsc.ar(note.midicps*(n+1),0,0.3)}).sum;
var env=EnvGen.kr(Env.perc(0.01,1.2), doneAction:2);
Out.ar(out, sig*env*amp!2);
}).add;
(
var matrix, index, ind, notes, times, n, a;
notes = [48, 53, 52, 57, 53, 59, 60] + 12;
times = [1/2, 1/2, 1, 1/2, 1/2, 1, 1]*0.5;
n = 7;
matrix = Array.fill(n,{Array.fill(n, {rrand(0, n-1);})});
index = (0..(n-1));
a = Prout({
inf.do({
ind = [];
matrix.collect({|row|
ind = ind ++ [(row * index).sum % n];
((row * index).sum % n).yield;
});
index = ind;
});
});
Pbind(*[\instrument: \mall, \index: a, \note: Pfunc({|ev| notes[ev[\index]];}), \dur:Pfunc({|ev|
times[ev[\index]];})]).trace.play;
)
s.quit;
represents a “sonification” of the probability distribution of finding a matrix A with the properties above, for p=7. We are assuming that the various matrices have equal probability to be generated in the code above.
So, how does this sound?
Like this
Audio clip: Adobe Flash Player (version 9 or above) is required to play this audio clip. Download the latest version here. You also need to have JavaScript enabled in your browser.
*By the way, you should check out the life of Galois, just to crush all your stereotypes about mathematicians. 😉
**Mathematicians love these “dual” definitions.
***Apart from the identity matrix and elements of P themselves, clearly.
